(a) Show that satisfies the time dependent Schrdinger equation for the harmonic oscillator potential (Equation 2 44) Here is any real constant with the dimensions of length (b) Find (x, t) 2 , and describe the motion of the wave packet (c) Compute (x) and (P), and check that Ehrenfests theorem (Equation 1 38) is satisfied 1 p 201 ( x 2 (1 ) the exp 2 m y (x, t) (1751) mo 1 4 jast 2xore

Question: (a) Show that satisfies the time-dependent Schrdinger equation for the harmonic oscillator potential (Equation 2.44). Here is any real constant with the dimensions of length.

(a) Show that

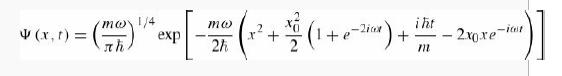
1* p [ 201 ( x + 2 (1 + ) +

satisfies the time-dependent Schrödinger equation for the harmonic oscillator potential (Equation 2.44). Here is any real constant with the dimensions of length.
(b) Find |Ψ (x, t)|², and describe the motion of the wave packet.
(c) Compute (x) and (P), and check that Ehrenfest’s theorem (Equation 1.38) is satisfied.

1* p [ 201 ( x + 2 (1 + ) + the exp 2 m y (x, t) = (1751) mo 1/4 -jast 2xore-

Step by Step Solution

★★★★★

3.47 Rating (167 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

a b The wave packet is a Gaussian of fixed shape whose center oscillates back and ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Introduction To Quantum Mechanics Questions!

FOSSIL IDENTIFICATION KEY Identify the names of the two fossils? Select the names of the two unique fossils that you identified from the snapshots located on the Parv Bed, and then click "Submit...

A simple harmonic oscillator takes 12.0 s to undergo five complete vibrations. Find (a) The period of its motion, (b) The frequency in hertz, and (c) The angular frequency in radians per second.

For the ground-level harmonic oscillator wave function (x) given in Eq. (40.24), | |2 has a maximum at x = 0. (a) Compute the ratio of | |2 at = +A to | |2 at x = 0, where A is given by Eq. (40.27)...

A simple harmonic oscillator at the point x = 0 generates a wave on a rope. The oscillator operates at a frequency of 40.0 Hz and with an amplitude of 3.00 cm. The rope has a linear mass density of...

Consider a time-independent Hamiltonian for a particle moving in one dimension that has stationary states n(x) with energies E n . (a) Show that the solution to the time-dependent Schrdinger equation...

(a) Using the potential energy U = 1/2m 2 x 2 , develop the Schrdinger equation for the harmonic oscillator. (b) Show by substitution that 0 (x) = A 0 e -a^2x^2/2 satisfies your equation, where 2 =...

Suppose where is some positive constant with the appropriate dimensions. Wed like to find the bound statessolutions to the time-independent Schrdinger equation with negative energy (E

Write a program that numerically solves the ground state energy and wavefunction of one- dimensinal Schrdinger equation for a given potential energy profile. Use "inverse power iteration" method....

the equation of dicplqment, velocity and acceloration for Simple harmonic motion . Can you simplify these equation step by step by using the famous symbols such as dx / dt rather than x ^ ....

Displacement in Simple Harmonic Motion The behaviour of a simple harmonic oscillator is expressed in terms of its displacement x from equilibrium, its velocity x , and its acceleration x at any given...

Oscillations Goal: The goal of this mini-project is to design a suspension system for a car. There are two essential components for such a system: springs and shock absorbers. Youre going to write a...

Anne is farsighted; the nearest object she can see clearly without corrective lenses is 2.0 m away. It is 1.8 cm from the lens of her eye to the retina. (a) Sketch a ray diagram to show...

P/E capital spend/share long term debt (000s) shares (000s) earnings per share working capital (000s) depreciation (000s) weighted aver cost of capital PV factor for FCFF tax rate 2020 (actual) 16.00...

Problem 3 - 1 Calculating Liquidity Ratios [ LO 2 ] SDJ , Incorporated, has net working capital of $ 2 , 1 6 0 , current liabilities of $ 5 , 5 1 0 , and inventory of $ 1 , 2 4 0 . What is the...

Prove that the posterior odds ratio of one hypothesis to another is equal to the product of the prior odds ratio and the likelihood ratio.

Set up a spreadsheet to reproduce Figure 4-15. Add error bars: Follow the procedure on page 90. Use s y for the and + error. Figure 4-15 3 10 m 0.6154 1.3462" style="" class="fr-fic fr-dib"> A B D F...

Excel LINEST function. Enter the following data in a spreadsheet and use LINEST to find slope, intercept, and standard deviations. Use Excel to draw a graph of the data and add a trendline. Draw...

Using the linear calibration curve in Figure 4-13, find the quantity of unknown protein that gives a measured absorbance of 0.264 when a blank has an absorbance of 0.095. Figure 4-13 0.40 Unknown...

Edelman Engines has $17 billion in total assets of which cash and equivalents total $120 million. Its balance sheet shows $2.55 billion in current liabilities of which the notes payable balance...

Carol Carpet manufactures broadloom carpet in seven processes: spinning, dyeing, plying, spooling, tufting, latexing and shearing. In the Dyeing Department, direct materials(dye) are added at the...

Nonconstant growth valuation Hart Enterprises recently paid a dividend, D0, of $2.25. It expects to have nonconstant growth of 17% for 2 years followed by a constant rate of 4% thereafter. The firm's...