Two noninteracting particles (of equal mass) share the same harmonic oscillator potential, one in the ground state and one in the first excited state.

(a) Construct the wave function, Ψ(x₁,x₂), assuming

(i) They are distinguishable, 

(ii) They are identical bosons, 

(iii) They are identical fermions. Plot |Ψ(x₁,x₂)|² in each case (use, for instance, Mathematica’s Plot3D).
(b) Use Equations 5.23 and 5.25 to determine ((x₁ - x₂)²) for each case.
(c) Express each Ψ(x₁,x₂) in terms of the relative and center-of-mass coordinates r Ξ x₁ - x₂  and R Ξ (x₁ + x₂)/2, and integrate over R to get the probability of finding the particles a distance |r| apart:

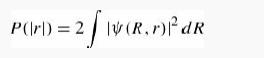(the 2 accounts for the fact that r could be positive or negative). Graph P(r) for the three cases.
(d) Define the density operator by

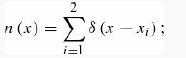
(n(x)) dx is the expected number of particles in the interval dx. Compute (n(x)) for each of the three cases and plot your results. (The result may surprise you.)

Equations 5.23

Equations 5.25

P(r) = 2 | (R.r) dr