Consider the skewness functional given by [T(F)=int_{-infty}^{infty}left[t-int_{-infty}^{infty} t d F(t)ight]^{3} d F(t)] where (F in mathcal{F}), a
Question:
Consider the skewness functional given by
\[T(F)=\int_{-\infty}^{\infty}\left[t-\int_{-\infty}^{\infty} t d F(t)ight]^{3} d F(t)\]
where \(F \in \mathcal{F}\), a collection of distribution functions with mean \(\mu\) and variance \(\sigma^{2}\) and third central moment \(\gamma\).
a. Using the method demonstrated in Example 9.8, write this functional in a form suitable for the application of Theorem 9.1.
b. Using Theorem 9.1, find the first two Gâteaux differentials of \(T(F)\).
c. Determine whether Corollary 9.1 applies to this functional and derive the asymptotic normality of \(T\left(\hat{F}_{n}ight)\) if it does.


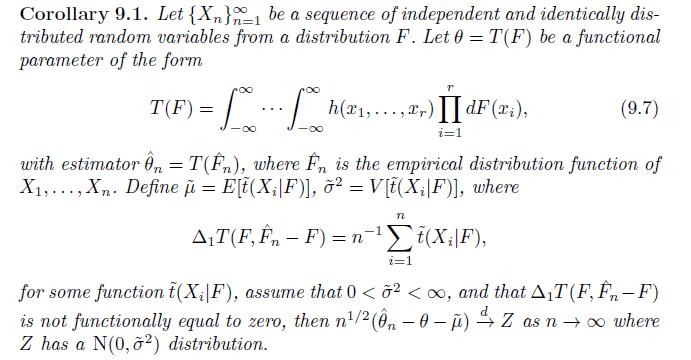
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





