Suppose that (X) is a discrete random variable that takes on positive integer values and has characteristic
Question:
Suppose that \(X\) is a discrete random variable that takes on positive integer values and has characteristic function
\[\psi(t)=\frac{p \exp (i t)}{1-(1-p) \exp (i t)}\]
Use Theorem 2.29 to find the probability that \(X\) equals \(k\) where \(k \in\) \(\{1,2, \ldots\}\).
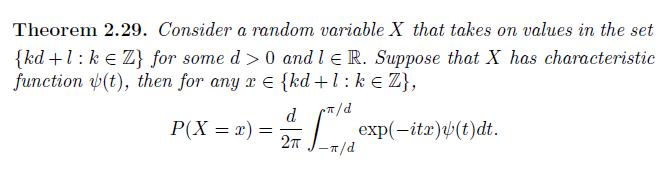
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





