Write a program in (mathrm{R}) that generates (b) samples of size (n) from a specified distribution (F)
Question:
Write a program in \(\mathrm{R}\) that generates \(b\) samples of size \(n\) from a specified distribution \(F\) (specified below). For each sample compute the statistic \(Z_{n}=n^{1 / 2} \sigma^{-1}\left(\bar{X}_{n}-\muight)\) where \(\mu\) and \(\sigma\) correspond to the mean and standard deviation of the specified distribution \(F\). Produce a density histogram of the \(b\) values of \(Z_{n}\). Run this simulation for \(n=10,25,50\), and 100 for each of the distributions listed below. On each histogram overlay a plot of the standard normal density and the function given by the one-term Edgeworth expansion for each case studied. Discuss how these histograms compare to what would be expected for large \(n\), as regulated by the underlying theory given by Theorems 4.20 and 7.4.
a. \(F\) corresponds to a \(\mathrm{N}(0,1)\) distribution.
b. \(F\) corresponds to an Exponential(1) distribution.
c. \(F\) corresponds to a \(\operatorname{Gamma}(2,2)\) distribution.
d. \(F\) corresponds to a \(\operatorname{UnIFORm}(0,1)\) distribution.
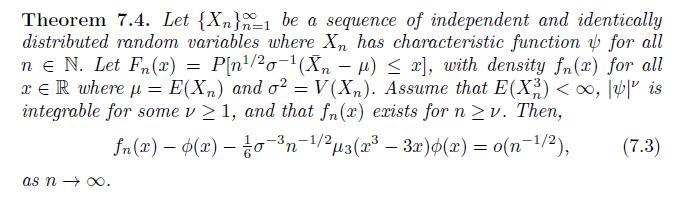
Step by Step Answer:





