In Example 17.11, assume that the promised amounts to \(A\) and \(B\) are \(\$ 110\) and \(\$ 90\), respectively. Develop the new table of results. What are the prices of \(A\) and \(\mathrm{B}\) ?

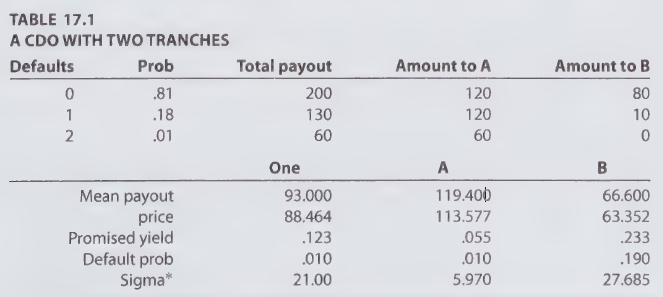
Transcribed Image Text:

Example 17.11 (Two are not always equal) Consider a CDO pool consisting of just two bonds, each of face value $100 million. The bonds are identical in structure, and their risk-neutral defaults are independent, with probabilities each equal to q = 10%. Using a simplified analysis we show how, by defining two tranches, the risk characteristics can be changed so that one tranche is less risky and the other is more risky than either would be if treated separately. We label the two tranches A and B. The combined face value is $200 million. Of this, $120 million is allocated to A and $80 million is allocated to B. However, A is considered the senior tranche and is paid first, up to A's promised amount. What remains is paid to B. In the event of a default, the recovery rate is 30%. The risk-free interest rate is 5%. Maturity is in 1 year. The entire situation and analysis is summarized in the Table 17.1. There are three scenarios corresponding to either zero, one, or two defaults. The risk-neutral