Find bases for the kernel and range of the linear transformations T in the indicated exercises. In each case, state the nullity and rank of T and verify the Rank Theorem.

Exercise 2

Data From Exercise 2

Let be defined by T : M₂₂ †’ R be defined by T(A) = tr (A).

(a) Which, if any, of the following matrices are in ker(T)?

(i)

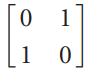
(ii)

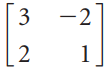
(iii)

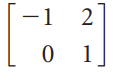
(b) Which, if any, of the following scalars are in range(T)?

(i) 0 

(ii) 5

(iii) -ˆš2

(c) Describe ker(T) and range(T).

3 -2 2 1