Modeling the movements in the exchange rate Equation (20.5) provides insight into the movements of nominal exchange rates between a domestic and a foreign country. Remember that the time periods in equation can refer to any time unit. The equation is:

\[
E_{t}=\frac{\left(1+i_{t}ight)\left(1+i_{t+1}^{e}ight) \cdots\left(1+i_{t+n}^{e}ight)}{\left(1+i_{t}^{*}ight)\left(1+i_{t+1}^{* e}ight) \cdots\left(1+i_{t+n}^{* e}ight)} E_{t+n+1}^{e}
\]

Equation 20. 5

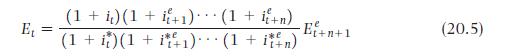
a. Suppose we are thinking of one-day time periods. There are overnight (1-day) interest rates. How do we interpret a large movement in the exchange rate over the course of the day if we do not observe any change in the 1-day interest rate?

b. We learned in Chapter 15 that a one-month (30- or 31-day interest rate) is the average of today's 1-day rate and the expected 1-day rates over the next 30 days. This will be true in both countries. The following headline is observed on February 1: "ECB predicted to cut interest rates February 14, dollar rises." Does the headline make sense?

c. We learned in Chapter 15 that a two-year bond yield is the average of today's one-year interest rate and the expected one-year rate one year from now. This will be true in both countries. The following headline is observed on February 1: "Fed announces that interest rates will remain low for the foreseeable future, dollar falls." Does the headline make sense?

d. The current account is this period's lending to (if positive) or borrowing from (if negative) the rest of the world. Assume the current account is more negative than expected and this is surprising news. Explain why the exchange rate would depreciate on this surprising news.

Transcribed Image Text:

Et = (1 + i)(1+i+1)* (1+it+n) (1 + i)(1+it+1)... (1 +it+n) -Et+n+1 (20.5)