Transform the time dependent version of the Black–Scholes equation

(a.k.a the Black–Scholes–Merton equation):

to log space xt = log St, and τ = T − t. Consider now the Fourier transform of the option price:

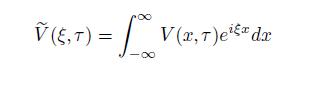
and the inverse transform:

where V (x, 0) is the payoff of the option at expiry in x. Apply (1.19)
to the transformed equation derived above to show that:

where  By considering the solution forflat rates, dividend yield and volatility, show that the solution to the call payoff is given by the Black–Scholes formula with implied rate, dividend yield and volatility given by:

Transcribed Image Text:

av - t +[r(t) q(t)]St av + 20 (t) S2 02V as2 - r(t)V(t) = 0