In Equation (3.153), we saw a linear version of an epidemic model. The commonly used nonlinear SIR
Question:
In Equation (3.153), we saw a linear version of an epidemic model. The commonly used nonlinear SIR model is given by
\[\begin{align*} \frac{d S}{d t} & =-\beta S I \\ \frac{d I}{d t} & =\beta S I-\gamma I \\ \frac{d R}{d t} & =\gamma I \tag{4.88} \end{align*}\]
where \(S\) is the number of susceptible individuals, \(I\) is the number of infected individuals, and \(R\) is the number who have been removed from the other groups, either by recovering or dying.
a. Let \(N=S+I+R\) be the total population. Prove that \(N=\) constant. Thus, one need only solve the first two equations and find \(R=N-S-I\) afterward.
b. Find and classify the equilibria. Describe the equilibria in terms of the population behavior.
c. Let \(\beta=0.05\) and \(\gamma=0.2\). Assume that in a population of 100 there is one infected person. Numerically solve the system of equations for \(S(t)\) and \(I(t)\) and describe the solution being careful to determine the units of population and the constants.
d. The equations can be modified by adding constant birth and death rates. Assuming these rates are the same, one would have a new system.
\[\begin{align*} \frac{d S}{d t} & =-\beta S I+\mu(N-S) \\ \frac{d I}{d t} & =\beta S I-\gamma I-\mu I \\ \frac{d R}{d t} & =-\gamma I-\mu R \tag{4.89} \end{align*}\]
How does this affect any equilibrium solutions?
e. Again, let \(\beta=0.05\) and \(\gamma=0.2\). Let \(\mu=0.1\) For a population of 100 with one infected person, numerically solve the system of equations for \(S(t)\) and \(I(t)\) and describe the solution being careful to determine the units of populations and the constants.
Data from 3.153
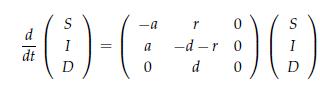
Step by Step Answer:

A Course In Mathematical Methods For Physicists
ISBN: 9781138442085
1st Edition
Authors: Russell L Herman





