Consider a chooser option that entitles the holder to choose, on the choice date T c periods from now, whether the option is a European call with exercise price X 1 and time to expiration T 1 T c or a European put with exercise price X 2 and time to expiration T 2 T c Show that the price of the cho...

The Answer is in the image, click to view ...

Consider a chooser option that entitles the holder to choose, on the choice date T c periods

Question:

Consider a chooser option that entitles the holder to choose, on the choice date T_c periods from now, whether the option is a European call with exercise price X₁ and time to expiration T₁ − T_c or a European put with exercise price X₂ and time to expiration T₂ − T_c. Show that the price of the chooser option at the current time (taken to be time zero) is given by (Rubinstein, 1992)

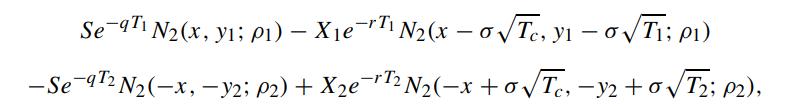Se-T1 N(x, y; 01) - Xe-T N(x - o Te, y - 0T1; 0) -Se-9T2 N(x, -Y2; P2) + Xe- N(x+0Tc-y2 + o T2; P2), where q is the continuous dividend yield of the underlying asset. The parameters are defined by

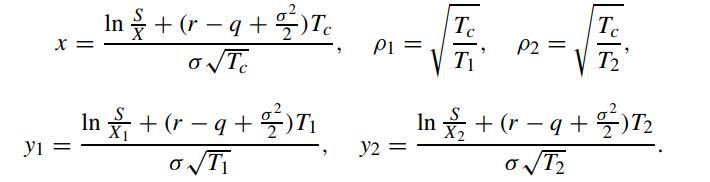
y X = In +(r - q+2) Tc OTc In +(r - q+)T o T1 1--9-- y2 = In + (r-q+)7 0T

Here, X solves the following nonlinear algebraic equation

Xe-9(T-Tc) N (21) - Xe-r(T-Tc) N (2-0T1 - Tc) + Xe q(T2-Tc) N (-22) - Xe-(T2-Tc) N(-22 +0 T - Tc) = 0, where

The two overlapping standard Brownian increments Z(T_c) and Z(T₁) have the joint normal distribution with zero means, unit variances and correlation coefficient Te T Te < T1.