Consider a portfolio containing t units of the risky asset and M t dollars of the

Consider a portfolio containing Δ_t units of the risky asset and M_t dollars of the riskless asset in the form of a money market account. The portfolio is dynamically adjusted so as to replicate an option. Let S_t and V (S_t,t) denote the price process of the underlying asset and the option value, respectively. Let r denote the riskless interest rate and Π_t denote the value of the self-financing replicating portfolio. When the self-financing trading strategy is adopted, we obtain

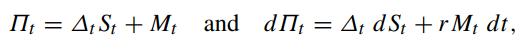where r is the riskless interest rate. Explain why the differential term S_t dΔ_t does not appear in dΠ_t . The asset price dynamics is assumed to follow the Geometric Brownian process:

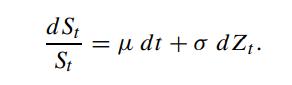In order that the option value and the value of the replicating portfolio match at all times, show that the number of units of asset held is given by

How should we proceed in order to obtain the Black–Scholes equation for V ?

Transcribed Image Text:

Пt = At St + Mt and dt = dПt At dSt +rMt dt,