Consider the extended CIR model where the short rate, r_t ≥ 0, follows the process

for some smooth deterministic functions α(t),β(t) and σ(t) > 0, and Z_t is a Brownian process under the risk neutral measure. Show that the bond price function is given by (Jamshidian, 1995)

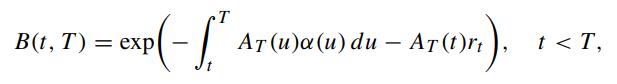
where A_T (t) satisfies the Ricatti equation

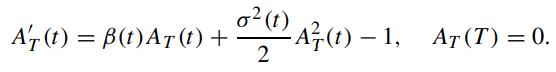
Also, show that the instantaneous T -maturity forward rate f (t,T ) is given by 

Transcribed Image Text:

drt = [a(t) - B(t)r₁]dt + o(t) √r, dZt