Consider the HullWhite model where the short rate is defined by Suppose we define a new variable x(t) where Also, show that the bond price B(t,T ) can be expressed as (Kijima and Nagayama, 1994) dr(t) (t) ar (t) dto dz(t) ...

The Answer is in the image, click to view ...

Consider the HullWhite model where the short rate is defined by Suppose we define a new variable

Question:

Consider the Hull–White model where the short rate is defined by

Suppose we define a new variable x(t) where

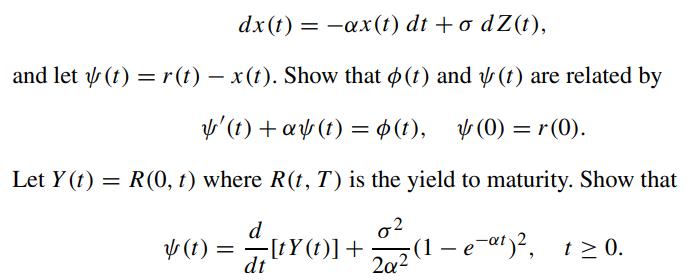
dx (t) = -ax(t) dt + o dZ(t), and let (t) = r(t) = x(t). Show that (t) and (t) are related by - '(t) + ay(t)

Also, show that the bond price B(t,T ) can be expressed as (Kijima and Nagayama, 1994)

B(0, T) B(0, t) 0 + 43 {1-[2-e-a(T-1)]+ (2 - e- - (2 eat)}. In B(t, T) In + - - - [e-a (T-1) e-(Tt) 1][r(t)

Fantastic news! We've Found the answer you've been seeking!

Step by Step Answer:

Related Book For book-img-for-question

Mathematical Models Of Financial Derivative

ISBN: 9783642447938

2nd Edition

Authors: Yue-Kuen Kwok

See More Books

Question Posted: Dec 04, 2023 05:22 AM

See More Questions

KYC's stock price can go up by 15 percent every year, or down by 10 percent. Both outcomes are equally likely. The risk free rate is 5 percent, and the current stock price of KYC is 100. (a) Price a...
1. Suppose that 10 years ago you purchased a car at $27,000 and the car was traded in today for $1,000. What is the depreciation rate? Suppose that the car is continuously discounting its value....
The vortex tube (also known as a Ranque or Hirsch tube) is a device that produces a refrigeration effect by expanding pressurized gas such as air in a tube (instead of a turbine as in the reversed...
Given a circularly linked list L containing an even number of nodes, describe how to split L into two circularly linked lists of half the size.
Which one of the following statements is false? a. Economic profit is less than or equal to net operating profit. b. A company that has a high quantity of one type of inventory may incur opportunity...
Listed below are the amounts (dollars) it costs for marriage proposal packages at the different Major League Baseball stadiums. Five of the teams don't allow proposals. Are there any outliers, and...
Apply the concepts and ideas in this chapter in order to develop a change management plan. This plan should focus on assessing the organizations willingness and ability to change, developing a change...
The federal governments consolidated nancial statements contained the following excerpt from a note entitled Veterans Compensation and Pension: The Department of Veterans Affairs (VA) has a liability...
how do you do this? Relevant data from the Poster Company's operating budgets are: Quarter 1 Quarter 2 Sales $208,470 $211,538 Direct material purchases 115,290 120,832 Direct labch 75,210 73,299...
Hull and White (1994) proposed the following two-factor short rate model whose dynamics under the risk neutral measure are governed by where u has an initial value of zero and follows the process The...
Consider the continuous time equivalent of the HoLee model as a degenerate case of the HullWhite model, where the diffusion process for the short rate r t under the risk neutral measure Q is given by...
When actual expenditures are less than budgeted expenditures, is the variance favorable or unfavorable?
From a square whose side has length $x$, measured in inches, create a new square whose side is 5 in. longer. Find an expression for the difference between the areas of the two squares as a function...
Sketch the requested conic sections in Problems 14-23 using the definition. A circle with radius 5
Find the present value of the ordinary annuities in Problems 21-32. Amount of Deposit m 23. $250 Frequency n semiannually Rate r 8% Time t 30 yr
Characterize the types of investments that are most vulnerable to political risk. Characterize those that are least vulnerable. What factors influence an investments vulnerability? On a scale of 1 to...
Refer to the following tree diagram for a two-stage experiment. Find the probabilities in Problems 1-6. $P(B) $ E E A B C A B C
For [w,x,y,:) determine the number string in of length 5 (a) that start with r; (b) with precisely iwo w's; (C) with no w's; (d) with an even number of ws.
Proposals have been made to ?sail? spacecraft to the outer solar system using the pressure of sunlight, or even to propel interstellar spacecraft with high-powered, Earth-based lasers. Sailing...
Identify the three basic third-party roles in negotiation.
Identify the six key elements that define an organizations structure.
Describe the characteristics of a bureaucracy.
Berbice Inc. has a new project, and you were recruitment to perform their sensitivity analysis based on the estimates of done by their engineering department (there are no taxes): Pessimistic Most...
#3) Seven years ago, Crane Corporation issued 20-year bonds that had a $1,000 face value, paid interest annually, and had a coupon rate of 8 percent. If the market rate of interest is 4.0 percent...
I have a portfolio of two stocks. The weights are 60% and 40% respectively, the volatilities are both 20%, while the correlation of returns is 100%. The volatility of my portfolio is A. 4% B. 14.4%...

Consider the HullWhite model where the short rate is defined by Suppose we define a new variable

Question:

dr(t) = [(t) - ar (t)] dto dz(t).

Step by Step Answer:

Mathematical Models Of Financial Derivative

Students also viewed these Business questions