Consider the pair of American call and put options with the same time to expiry and

Consider the pair of American call and put options with the same time to expiry τ and on the same underlying asset. Assume the volatility of the asset price to be at most time dependent. Let S_C and S_P be the spot asset price corresponding to the call and put, respectively (S_C and S_P need not be the same since the calendar times at which we are comparing values need not be the same). Suppose the two options have the same moneyness, that is,

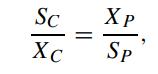where X_C and X_P are the strike price corresponding to the call and put, respectively. Let C(S_C,τ ; X_C,r,q) and P(SP ,τ ; XP ,r,q) denote the price function of the American call and put, respectively. Derive the generalized put-call symmetry relation (Carr and Chesney, 1996)

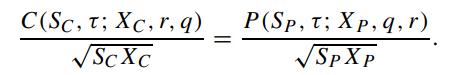
Furthermore, let S^∗_C (τ ; X_C,r,q) and S^∗_P (τ ; X_P ,r,q) denote the optimal exercise price of the American call and put, respectively. Show that

This relation is a generalization of the result given in (5.1.16). 

Transcribed Image Text:

Sc Xp Xc Sp =