Let P(S, ; X,r,q) denote the price function of an American put option. Show that P(X, ;
Question:
Let P(S,τ ; X,r,q) denote the price function of an American put option. Show that P(X,τ ; S,q,r) also satisfies the Black–Scholes equation:
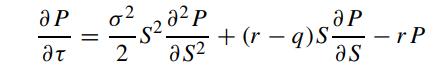
together with the auxiliary conditions:
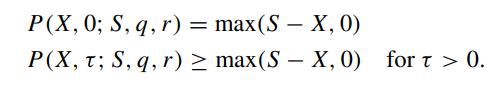
Note that the auxiliary conditions are identical to those of the price function of the American call option. Hence, we can conclude that
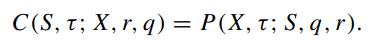
![1 P ( 13 1: 7, 9, 1) = X PCX T; SX Write P (S', T) = P that 02 -[SXP (S', T)] - a T as2 [SXP (S', T)] - (r](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1700/5/4/6/207655c469fbddb71700546202712.jpg)
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





