We would like to examine the credit yield spreads of the floating rate debt and fixed rate debt under the Merton risky bond model with stochastic interest rate (Ikeda, 1995). Let A_t and r_t denote the firm asset value and short rate, respectively, whose dynamics are governed by

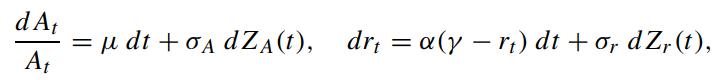
and dZ_A dZ_r = ρ dt. For the defaultable fixed rate debt, the payoff at debt’s maturity T is given by min(A_T ,F), where F is the fixed par value. However, the par at maturity of a floating rate debt is stochastic, whose value is given by 

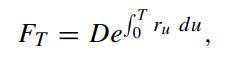
for some constant D. The stochastic par is equivalent to the value of the money market account invested for T years with initial deposit D. Let B(r,t; T) denote the price of the corresponding default free discount bond and let σ_B(r, t; T) denote the corresponding bond volatility.

(a) Show that the value of the defaultable fixed rate debt at the current time t conditional on A_t = A and r_t = r is given by

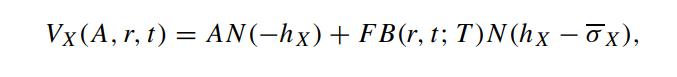where

(b) Write D_t = De∫^t₀ ^{r(u) du}, which is known at time t from the actual realization of the interest rate process from 0 to t. Show that the value of the defaultable floating rate debt is given by

Interestingly, the bond volatility does not enter into V_L(A,r,t). Why?

Let Y(r,t; T) denote the value of the money market account with initial deposit D. The evolution dynamics of Y(t) are given by dY = r_tY dt. Use B(r,t; T) and Y(r,t; T) as the corresponding numeraire in the fixed rate debt and floating rate debt valuation, respectively.

Transcribed Image Text:

d At = μ dt + σA dZA (t), drt = a(y - rt) dt+ or dZr (t), At