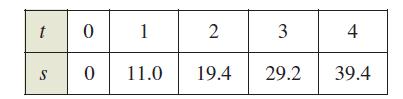
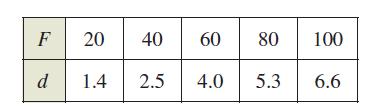
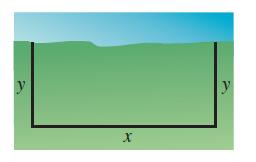
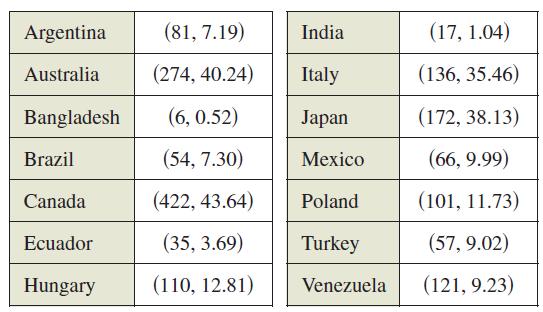
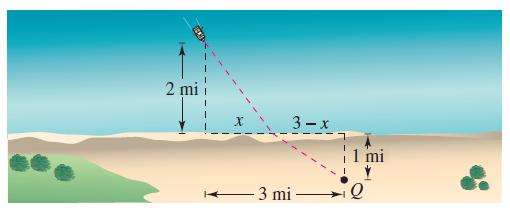
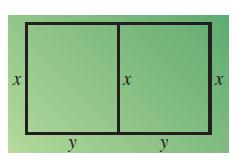
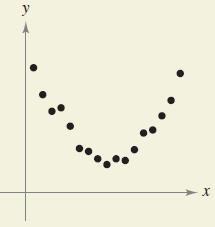
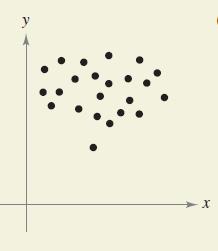
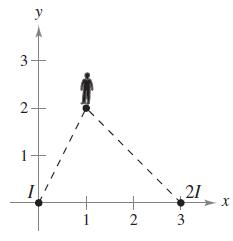
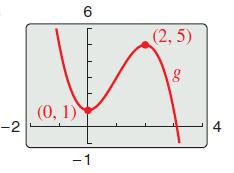
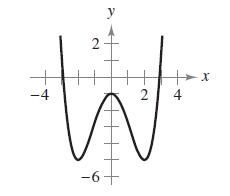
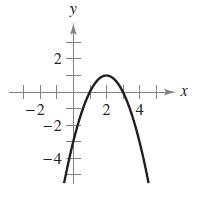
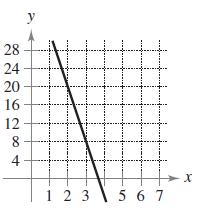
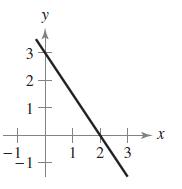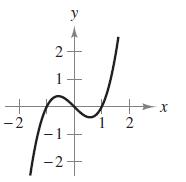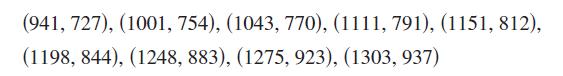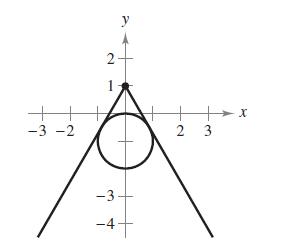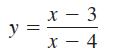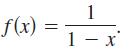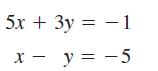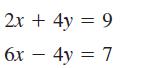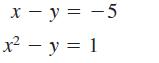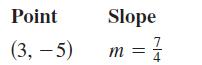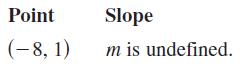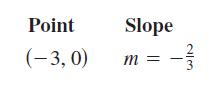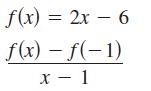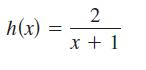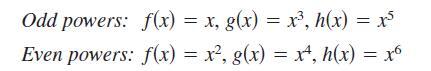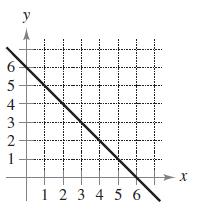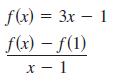Calculus 10th Edition Ron Larson, Bruce H. Edwards - Solutions
Unlock the full potential of your calculus study with our comprehensive resources for "Calculus 10th Edition" by Ron Larson and Bruce H. Edwards. Access our online answers key to find detailed solutions and explanations for every problem. With our solution manual and solutions PDF, you can explore solved problems and understand the step-by-step answers to enhance your learning. Our test bank and chapter solutions provide invaluable aid for exam preparation. Utilize the instructor manual to navigate the textbook effectively. Enjoy the convenience of free download options to have all questions and answers at your fingertips.
![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()