Refer to Matched Problem 1 in Section 9.1, where we found the following transition matrix for an insurance company:

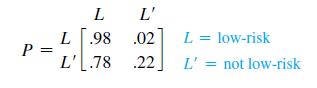
If these probabilities remain valid for a long period of time, what percentage of drivers are expected to be in the low-risk category during any given year?

Data from Matched Problem 1 in Section 9.1

An insurance company classifies drivers as low-risk if they are accident-free for one year. Past records indicate that 98% of the drivers in the low-risk category (L) one year will remain in that category the next year, and 78% of the drivers who are not in the low-risk category (L′) one year will be in the low-risk category the next year.

Draw a transition diagram.

Find the transition matrix P.

If 90% of the drivers in the community are in the low-risk category this year, what is the probability that a driver chosen at random from the community will be in the low-risk category next year? Year after next?

Transcribed Image Text:

P = = L L.98 L'78 L' 02 22 L = low-risk L' = not low-risk