When a gas expands reversibly, the work that it does on its surroundings is given by the integral

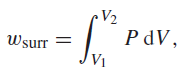
where V₁ is the initial volume, V₂ is the final volume, and P is the pressure of the gas. Certain nonideal gases are described by the van der Waals equation of state,

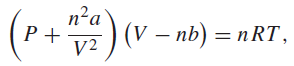
where V is the volume, n is the amount of gas in moles, T is the temperature on the Kelvin scale, and a and b are constants. R is usually taken to be the ideal gas constant, 8.3145 J K^ˆ’1 mol^ˆ’1.

(a) Obtain a formula for the work done on the surroundings if 1.000 mol of such a gas expands reversibly at constant temperature from a volume V₁ to a volume V₂.
(b) If T = 298.15 K,V1 = 1.00l (1.000 × 10^ˆ’3 m³), and V₂ = 100.0l = 0.100 m³, find the value of the work done for 1.000 mol of CO₂, which has a = 0.3640 Pa m⁶ mol^ˆ’2 and b = 4.267 × 10^ˆ’5 m³ mol^ˆ’1. The ideal gas constant, R = 8.3145 J K^ˆ’1 mol^ˆ’1.
(c) Calculate the work done in the process of part b if the gas is assumed to be ideal.

V2 P dV, Wsurr VI na P +: V2 (V nb) = n RT,