Let \((X, \mathscr{A})\) be a measurable space and \(\left(\mu_{n}ight)_{n \in \mathbb{N}}\) be a sequence of measures thereon. Set, as in Example 9.10(ii), \(\mu=\sum_{n \in \mathbb{N}} \mu_{n}\). By Problem 4.7(ii) this is again a measure. Show that
\[
\int u d \mu=\sum_{n \in \mathbb{N}} \int u d \mu_{n} \quad \forall u \in \mathcal{M}^{+}(\mathscr{A})
\]
[Instructions: (1) consider \(u=\mathbb{1}_{A}\); (2) consider \(u=f \in \mathcal{E}^{+}\); and (3) approximate \(u \in \mathcal{M}^{+}\) by an increasing sequence of simple functions and use Theorem 9.6. To interchange increasing limits/suprema use the hint to Problem 4.7(ii).]

Data from problem 4.7 (ii)

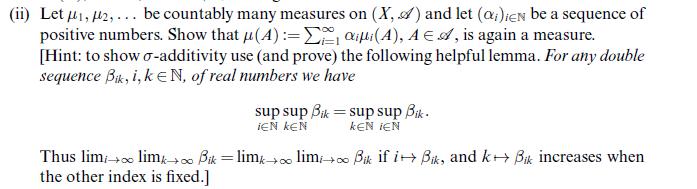
Data from example 9.10

Data from theorem 9.6

Transcribed Image Text:

(ii) Let u,2,... be countably many measures on (X, ) and let (a)ien be a sequence of positive numbers. Show that (4):= (A), AE A, is again a measure. [Hint: to show o-additivity use (and prove) the following helpful lemma. For any double sequence Bik, i, kEN, of real numbers we have sup sup Bik = sup sup Bik. EN KEN KEN IEN Thus limi limo Bik = limko limio Bik if i Bik, and k Bik increases when the other index is fixed.]