Use Jensen's inequality (Example 13.14 (i), (ii)) to derive Hlder's inequality and Minkowski's inequality. Use [Lambda(x)=x^{1 /
Question:
Use Jensen's inequality (Example 13.14 (i), (ii)) to derive Hölder's inequality and Minkowski's inequality. Use
\[\Lambda(x)=x^{1 / q}, x \geqslant 0, \quad w=|f|^{p} \quad \text { and } \quad u=|g|^{q}|f|^{-p} \mathbb{1}_{\{f eq 0\}}\]
for Hölder's inequality and
\[\Lambda(x)=\left(x^{1 / p}+1ight)^{p}, x \geqslant 0, \quad w=|f|^{p} \mathbb{1}_{\{f eq 0\}} \quad \text { and } \quad u=|f|^{-p}|g|^{p} \mathbb{1}_{\{f eq 0\}}\]
for Minkowski's inequality.
Data from example 13.14 (i)
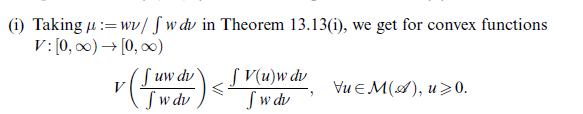
Data from example 13.14 (ii)
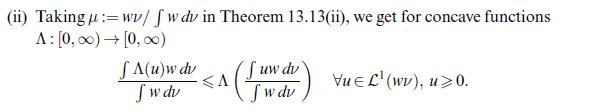
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





