Variants of Jensen's inequality. Let ((X, mathscr{A}, mu)) be a probability space. (i) Show Jensen's inequality for
Question:
Variants of Jensen's inequality. Let \((X, \mathscr{A}, \mu)\) be a probability space.
(i) Show Jensen's inequality for convex \(V: \mathbb{R} ightarrow \mathbb{R}\), see Example 13.14 (v).
(ii) Show Jensen's inequality for concave \(\Lambda: \mathbb{R} ightarrow \mathbb{R}\), see Example 13.14 (vi).
(iii) Let \(-\infty \leqslant a
For \(u: X ightarrow(a, b)\) such that \(u, V(u) \in \mathcal{L}^{1}(\mu)\) we have \(\int u d \mu \in(a, b)\) and \(V\left(\int u d \muight) \leqslant\) \(\int V(u) d \mu\).
(iv) Let \(-\infty \leqslant a
For \(u: X ightarrow(a, b)\) such that \(u, \Lambda(u) \in \mathcal{L}^{1}(\mu)\) we have \(\int u d \mu \in(a, b)\) and \(\int \Lambda(u) d \mu \leqslant\) \(\Lambda\left(\int u d \muight)\).
Data from example 13.14 (v)
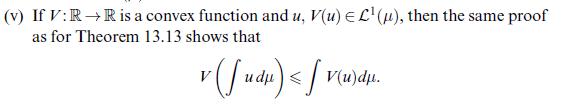
Data from example 13.14 (vi)
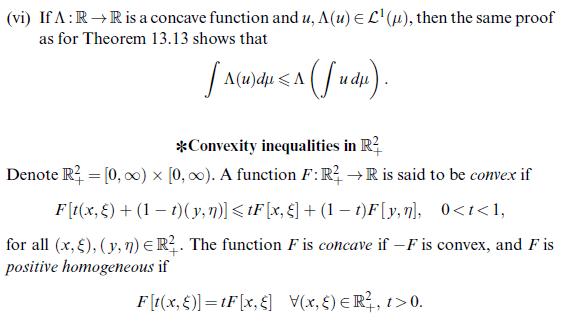
Step by Step Answer:






