Find the response of the freely vibrating system of Problem 7,

\[ \begin{aligned} m(\ddot{x} & \left.+\frac{L}{2} \ddot{\theta}\right)+\left(k_{1}+k_{2}\right) x \\ & +\left(k_{3}+k_{4}\right)(x+L \theta)=0 \\ \frac{m L}{2} \ddot{x}+ & \left(I_{O}+m \frac{L}{2}\right) \ddot{\theta}+\left(k_{3}+k_{4}\right)(x+L \theta) L \\ & +m g \frac{L}{2} \theta+K \theta=0 \end{aligned} \]

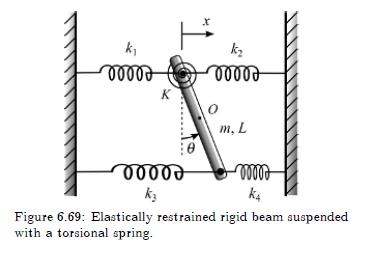
Problem 7:

Derive the equation of motion for the elastically restrained rigid beam shown in Figure 6.69 using

(a) Newton's second law, and

(b) Lagrange's equation.

Transcribed Image Text:

k 00000 K k 00000 eeeee ? K3 m, L eelle K4 Figure 6.69: Elastically restrained rigid beam suspended with a torsional spring.