In Problem 6, using the governing equations of motion given below, assume a harmonic base motion and find the undamped response:

\[ \begin{aligned} (m+M) \ddot{x}+M l\left(\ddot{\theta} \cos \theta-\dot{\theta}^{2} \sin \theta\right) & \\ -k(y-x)-c(\dot{y}-\dot{x}) & =0 \\ \left(I_{G}+M l^{2}\right) \ddot{\theta}+M l \ddot{x} \cos \theta & \\ +K \theta-M g l \sin \theta & =0 \end{aligned} \]

Problem 6:

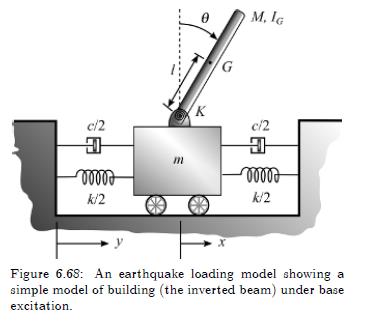
A simple lumped-parameter model of a building, shown as the inverted link in Figure 6.68, can be used for preliminary study of earthquake dynamics. Derive the equations of motion for this two degreeof-freedom system using

(a) Newton's second law, and

(b) Lagrange's equation. Let \(y(t)\) be the prescribed ground motion, and \(x(t)\) be the absolute position of the mass \(m\).

c/2 00000 m k/2 M. IG K c/2 C 00000 k/2 Figure 6.68: An earthquake loading model showing a simple model of building (the inverted beam) under base excitation.