Suppose the system of Equation 6.38, [ begin{aligned} & {left[begin{array}{cc} m_{1} & 0 0 & m_{2}
Question:
Suppose the system of Equation 6.38,
\[ \begin{aligned} & {\left[\begin{array}{cc} m_{1} & 0 \\ 0 & m_{2} \end{array}\right]\left\{\begin{array}{l} \ddot{x}_{1} \\ \ddot{x}_{2} \end{array}\right\}} \\ & +\left[\begin{array}{cc} k_{11} & k_{12} \\ k_{21} & k_{22} \end{array}\right]\left\{\begin{array}{l} x_{1} \\ x_{2} \end{array}\right\}=\left\{\begin{array}{l} F_{1}(t) \\ F_{2}(t) \end{array}\right\} \end{aligned} \]
is forced by the vector \(\left\{F_{1}(t) \quad F_{2}(t)\right\}^{T}=\) \(\left\{f_{1} \cos \omega_{1} t \quad f_{2} \cos \omega_{2} t\right\}^{T}\). Solve for the general response using the direct method.
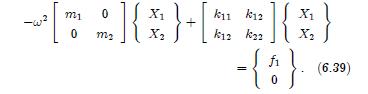
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Mechanical Vibration Analysis, Uncertainties, And Control
ISBN: 9781498753012
4th Edition
Authors: Haym Benaroya, Mark L Nagurka, Seon Mi Han
Question Posted:





