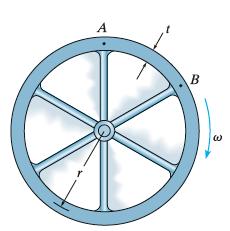
The rim on the flywheel has a thickness \(t\), width \(b\), and specific weight \(\gamma\). If the flywheel is rotating at a constant rate of \(\omega\), determine the maximum moment developed in the rim. Assume that the spokes do not deform. Due to symmetry of the loading, the slope of the rim at each spoke is zero. Consider the radius to be sufficiently large so that the segment \(A B\) can be considered as a straight beam fixed at both ends and loaded with a uniform centrifugal force per unit length. Show that this force is \(w=b t \gamma \omega^{2} r / g\).

Transcribed Image Text:

A B 3