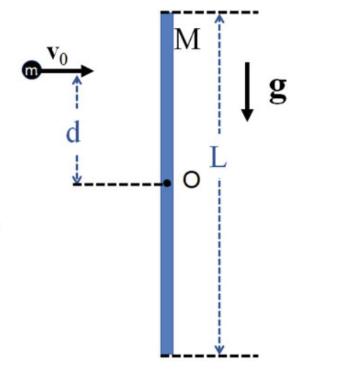
Consider the homogeneous bar, of negligible cross section, mass \(M=1.333 \mathrm{~kg}\) and length \(L=60.0 \mathrm{~cm}\) in Fig.12.19

. It is constrained to rotate in a vertical plane about its center of mass \(\mathrm{O}\), which for simplicity coincides with the origin of a reference system \((x, z)\). For times \(t

1. the angular speed \(\omega_{0}\) of the bar after the impact;

2. the impulse \(\Delta \mathbf{p}\) of the forces applied by the constraint at point \(\mathrm{O}\) to the bar during the impact (specify magnitude and direction).

3. Following the collision, the bar rotates without friction around O. Calculate the angular speed \(\omega_{1}\) of the bar when it is parallel to the horizontal axis (i.e., it has made a rotation of \(90^{\circ}\) ).
4. Show that the potential energy of the bar does not change if it is in a vertical position (as in the figure) or if it is parallel to the horizontal axis.

Fig. 12.19

Transcribed Image Text:

m E d M L g '