Time dilation and length contraction. Clock A is placed at the origin of the primed frame; it reads time \(t^{\prime}=0\) just as the origins of the primed and unprimed frames coincide. At a later time \(t\) to observers in unprimed frame, find from the Lorentz transformation of Eqs. 2.15

Data from Eqs. 2.15

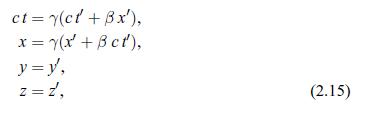
(a) how far A has moved, and

(b) what time A reads. This is an example of the fact that moving clocks run slow. A stick of length \(L_{0}\) is placed at rest along the \(x^{\prime}\) axis of the primed frame. Observers in the unprimed frame measure the position of both ends of the stick at the same time \(t\) to them as the stick is moving along at speed \(V\).

(c) Using the Lorentz transformation, find the length \(L \equiv\left(x_{2}-x_{1} \right)\) of the stick in the unprimed frame, in terms of \(L_{0}\) and the relative frame velocity \(V\). Here \(x_{2}\) and \(x_{1}\) are the locations of each end of the stick, as measured in the unprimed frame. The fact that \(L

Transcribed Image Text:

ct = (ct +x'), x=(x+Bot), y=y, z=1, (2.15)