Trajectory specialists plan to send a spacecraft to Saturn requiring a gravitational assist by Jupiter. In Jupiter's rest frame the spacecraft's velocity will be turned \(90^{\circ}\) as it flies by, as illustrated in Figure 7.15(a).

Data from Figure 7.15 (a) and (b)

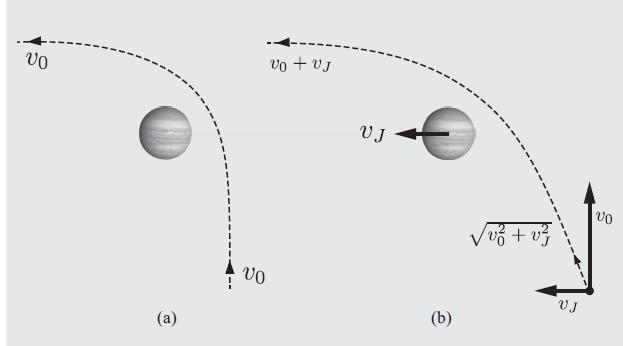
(a) If the nearest point on the spacecraft's path is a distance of \(2 R_{J}=140,000 \mathrm{~km}\) from the center of Jupiter, how fast (in \(\mathrm{km} / \mathrm{s}\) ) is the spacecraft's speed in Jupiter's frame when it is at this nearest point?

(b) In Jupiter's frame what is \(v_{0}\) (as shown in the figure), the spacecraft's speed (in \(\mathrm{km} / \mathrm{s}\) ) both long before and long after its encounter with Jupiter (but not so long before or after that its distance from the sun has changed appreciably)?

(c) Note that long after the encounter, in the sun's frame the velocity of the spacecraft is \(v_{0}+v_{J}\) along the direction of Jupiter's motion around the sun, as illustrated in Fig. 7.15(b). Is this velocity sufficient to take the spacecraft out to the orbit of Saturn? Explain. (Useful data: Jupiter has mass \(M_{J}=1.9 \times 10^{27} \mathrm{~kg}\) and radius \(R_{J}=70,000 \mathrm{~km}\). Its average orbital radius and velocity around the sun are about \(780 \times 10^{6} \mathrm{~km}\) and \(13 \mathrm{~km} / \mathrm{s}\), respectively. The average orbital radius of Saturn is \(1.4 \times 10^{9}\) \(\mathrm{km}\). Newton's gravitational constant is \(G=6.67 \times 10^{-11} \mathrm{~m}^{3} /\left(\mathrm{kg} \mathrm{s}^{2}.\right)\) )

Transcribed Image Text:

VO (a) VO VJ (b) - vz Vo VJ