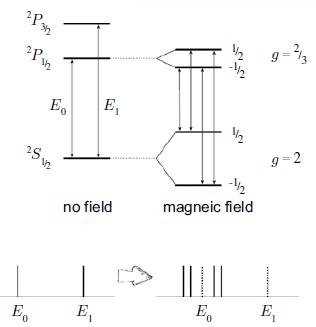
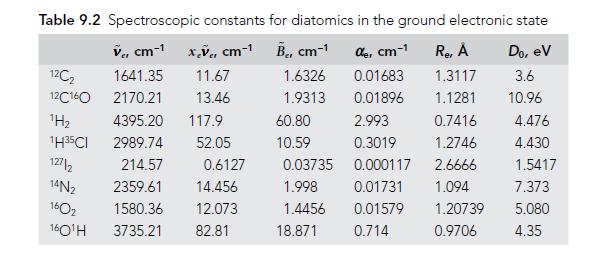
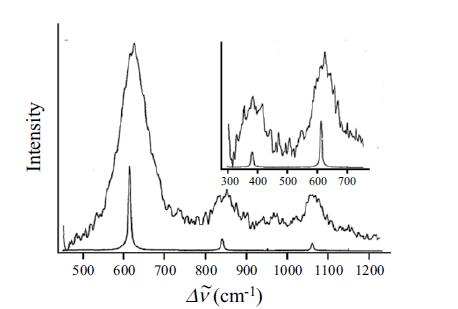
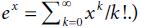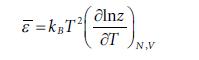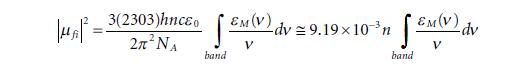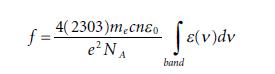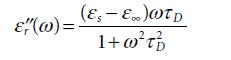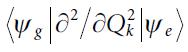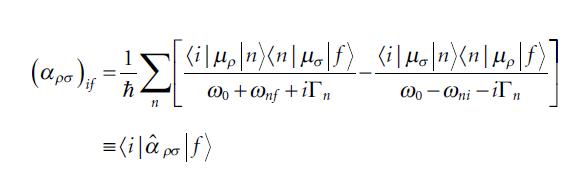Molecular Spectroscopy 2nd Edition Jeanne L McHale - Solutions

Discover comprehensive solutions to the challenging questions from "Molecular Spectroscopy 2nd Edition" by Jeanne L McHale. Access the online answers key and download solutions in PDF format for free. Dive into solved problems with detailed step-by-step answers and explore a complete solution manual designed to enhance your understanding. Benefit from the instructor manual and test bank, providing chapter solutions and a wealth of questions and answers tailored to this textbook. Whether you're a student or an educator, our resources offer invaluable support for mastering molecular spectroscopy concepts.