(a) Show that in the nonrelativistic limit, the components of the perfect-fluid stress energy tensor (13.85) take on the forms (13.91), and verify that these agree with the densities and fluxes of energy and momentum that are used in nonrelativistic fluid mechanics (Table 13.1).

(b) Show that the contribution of the pressure P to the relativistic density of inertial mass causes the term(P /ρ_N)_ρNv = Pv to appear in the nonrelativistic energy flux.

In Eq 13.85

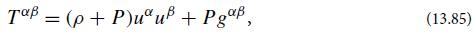
In Eq 13.91

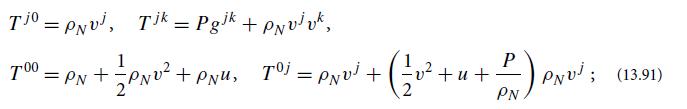
In Table 13.1

Ta = (p+P)u u + Pga, (13.85)