(a) Show that the parameter along the world line (24.69) is proper time and that the 4-acceleration has magnitude |a(vector)]= 1/. (b) Show that

(a) Show that the parameter τ along the world line (24.69) is proper time and that the 4-acceleration has magnitude |a(vector)]= 1/κ.

(b) Show that the unit vectors e(vector)_ĵ  introduced in Sec. 24.5.3 all obey the Fermi-Walker transport law(24.62) and therefore, by virtue of Eq. (24.61b), the proper reference frame built from them has vanishing rotation rate: Ω(vector) = 0.

(c) Show that the coordinates x^2̂ and x^3̂ introduced in Sec. 24.5.3 are equal to the y and z coordinates of the inertial frame used to define the observer’s world line [Eqs. (24.69)].

(d) Show that the proper-reference-frame coordinates constructed in Sec. 24.5.3 are related to the original {t , x, y, z} coordinates by

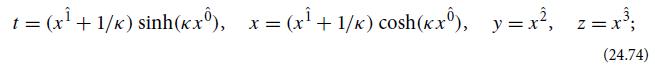
and from this, deduce the form(24.70) of the Minkowski spacetime metric in the observer’s proper reference frame.

(e) Show that, when converted to Rindler coordinates by moving the spatial origin, the coordinate transformation (24.74) becomes (24.72), and the metric (24.70) becomes (24.73).

(f) Show that observers at rest in the Rindler coordinate system(i.e., who move along world lines of constant {x' , y' , z'}) have 4-acceleration

Equations

t = (x+1/k) sinh (kx), x = (x+1/k) cosh (kx), y=x, z=x; (24.74)