Consider the pulsatile flow of blood through one of the bodys larger arteries. The pressure gradient dP/dz
Question:
Consider the pulsatile flow of blood through one of the body’s larger arteries. The pressure gradient dP/dz = P'(t) consists of a steady term plus a term that is periodic, with the period of the heart’s beat.
(a) Assuming laminar flow with v pointing in the z direction and being a function of radius and time, v = v(ω̅, t)ez, show that the Navier-Stokes equation reduces to ∂v/∂t =−P'/ρ + ν∇2v.
(b) Explain why v(", t) is the sum of a steady term produced by the steady (time independent) part of P', plus terms at angular frequencies ω0, 2ω0, . . . , produced by parts of P' that have these frequencies. Here ω0 ≡ 2π/(heart’s beat period).
(c) Focus on the component with angular frequency ω = nω0 for some integer n. For what range of ω do you expect the ω̅ dependence of ν to be approximately Poiseuille [Eq. (13.80)], and what ω̅ dependence do you expect in the opposite extreme, and why?
(d) By solving the Navier-Stokes equation for the frequency-ω component, which is driven by the pressure-gradient term
![]()
and by imposing appropriate boundary conditions at ω̅ = 0 and ω̅ = a, show that
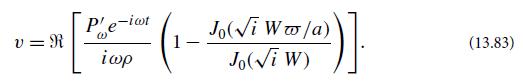
Here R means take the real part, a is the artery’s radius, J0 is the Bessel function, i is
![]()
is called the (dimensionless) Womersley number.
(e) Plot the pieces of this v(ω̅) that are in phase and out of phase with the driving pressure gradient. Compare with the prediction you made in part (b). Explain the phasing physically. Notice that in the extreme non-Poiseuille regime, there is a boundary layer attached to the artery’s wall, with sharply changing flow velocity. What is its thickness in terms of a and the Womersley number?
Eq. (13.80)
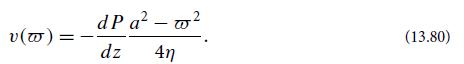
Step by Step Answer:

Modern Classical Physics Optics Fluids Plasmas Elasticity Relativity And Statistical Physics
ISBN: 9780691159027
1st Edition
Authors: Kip S. Thorne, Roger D. Blandford





