Drudes conductivity formula fails when the frequency is low and the mean time between electron

Drude’s conductivity formula fails when the frequency ω is low and the mean time τ between electron collisions is large. If v̅ is a characteristic electron speed, one says that the normal skin effect becomes anomalous when the mean distance between collisions ℓ = v̅τ exceeds the skin depth δ(ω). To study this regime, we first write the rate of change of an ohmic current density j(t) as the sum of a field-driven acceleration term dj/dt|_acc = (σ₀/τ)E and a collisional deceleration term dj/dt |_coll = −j/τ. This reproduces Ohm’s law in the steady state dj/dt = 0 because

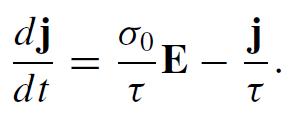
(a) Approximate dj/dt by ∂j/∂t and combine the foregoing with the Maxwell equations (neglecting the displacement current) to get a partial equation for B(r,t) which has only first-order time derivatives:

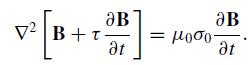
Let B(z, t) = B₀e^i(kz−ωt) and confirm that Drude’s frequency-dependent conductivity emerges from your dispersion relation k(ω).
(b) Drude’s conductivity formula overestimates the effect of collisions when ℓ >> δ. A phenomenological way to correct this exploits the convective derivative to write

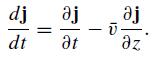
Derive a cubic equation which determines the new dispersion relation. Find k(ω) explicitly in the extreme anomalous limit (where the gradient term dominates) and show that

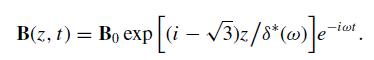
The anomalous skin depth δ^∗(ω) = 2(Λ²v̅/ω)1/3 found here describes experiments well in this regime. The constant 2 = m/μ₀ne².

(c) Show that 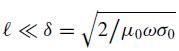is the condition to neglect the non-local gradient term.

Transcribed Image Text:

dj dt || 00 T E- j T