Let = A + (1/c 2 )/t. Fermi showed that one can use a

Let Ω = ∇ · A + (1/c²)∂ϕ/∂t. Fermi showed that one can use a Lagrange parameter λ to impose the Lorenz gauge condition Ω = 0 using the Lagrangian density

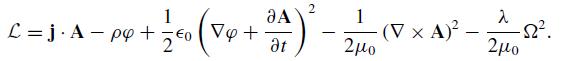
(a) Show that the Lagrange equations for the potentials are modified inhomogeneous wave equations.

(b) Find the corresponding modified inhomogeneous Maxwell equations.

(c) Manipulate the equations in (a) and use conservation of charge to deduce thatΩ satisfies a homogeneous wave equation.

(d) Find initial conditions for the wave equation in (c) which guarantee that the Lorenz gauge condition is always satisfied and that E and B in (b) are the physical electric and magnetic fields.

Transcribed Image Text:

1 C = j·A - ρφ + Ξε Στο Pot 2A at - 1 2μο (Π x A) λ 2μο Ω.