Let a transverse electromagnetic wave H = xH x exp i(ky t) propagate in a linear

Let a transverse electromagnetic wave H = x̂H_x exp i(ky − ωt) propagate in a linear magnetic medium exposed to a static magnetic field B = B_z ẑ. If γ and τ are constants, experiment shows that the induced magnetization obeys

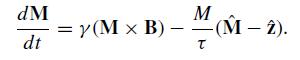
(a) The first term on the right describes precession of the magnetization vector. The second term on the right side accounts (phenomenologically) for loss mechanisms which drive the system toward equilibrium (where M is aligned with the external field). Confirm this claim by computing M(t) when γ = 0.

(b) Let ω²₀ = γ²μ₀B_zH_z and show that

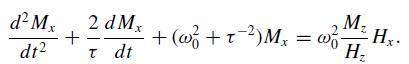
Use this information to find the real and imaginary parts of the complex magnetic permeability μ̂ (ω). Establish that the magnetic permeability of the system is

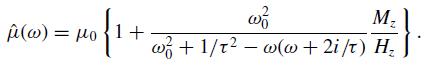
(c) Derive a wave equation for this medium and relate the real and imaginary parts of k to the real and imaginary parts of μ̂ and to (assumed real, positive, and constant). Prove that the amplitude of the H-wave given above decreases (increases) as it propagates if Mz/Hz is positive (negative).
Remark: Given the result in (c), amplification of the wave occurs only if we supply energy to “pump” the system into the higher energy state with M anti-parallel to H. This is the analog of producing a “population inversion” to initiate laser action in an active medium.

Transcribed Image Text:

dM dt = y(M x B) - - T -(M - 2).