Let C be the capacitance of capacitor formed from two identical, flat conductor plates separated by a distance d. The plates have area A and arbitrary shape. When d 0 = Aε₀/d.

(a) If δE = E − E0, prove the identity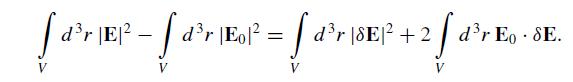

(b) Let E = −∇_ϕ be the actual field between the finite-area plates and let E₀ = −∇_ϕ0 be the uniform field that would be present if A were infinite. Use the identity in part (a) to prove that C > C₀ , using V as the volume between the finite-area plates. Assume that the potentials ϕ and ϕ₀ take the same (constant) values on the plates.

Eo . [dr E - [ dr Eat = [ar|8E + 2 [dr E- SE