Let the current density in a linear antenna of length h be

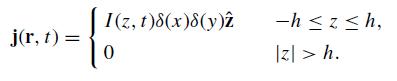
(a) Find E_rad(r, t) for the current I (z, t) = Aδ(t). Your answer will have two terms. Determine the apparent origin of each term and give an argument for the time delay between the two. Make a polar plot centered on the antenna and regard each ray as a time axis in units of t /τ where h = cτ. For each of the two terms above, draw a closed, dashed curve which indicates when the signals arrive at each angle. At a few representative angles, draw solid dots on the dashed curves to indicate the relative magnitude of E_rad at that angle.
(b) Repeat part (a) for the traveling-wave current I (z, t) = A̅ δ(t − z/c).
(c) Show that a uniform current I (z, t ) = A exp(−iωt) radiates total power P where

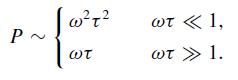
(d) Show that the traveling-wave current I (z, t) = A̅ exp i(kz − ωt) radiates total power P̅ where

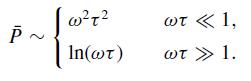
Some useful integrals are

where Ci(u) is the cosine integral and Si(u) is the sine integral.

Transcribed Image Text:

j(r, t) = { I(z, t)8(x)8(y)2 0 -h≤z≤h, |z|> h.