Question: Let the z-axis be the symmetry axis for an infinite number of identical rings, each with charge Q and radius R. There is one ring

Let the z-axis be the symmetry axis for an infinite number of identical rings, each with charge Q and radius R. There is one ring in each of the planes z = 0, z = ±b, z = ±2b, etc. Exploit the Fourier expansion in Example 1.6 to find the potential everywhere in space. Check that your solution makes sense in the limit that the cylindrical variable ρ >> R, b.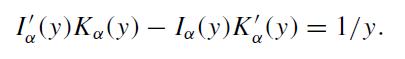 I(y)Ka(y) Ia(y)K'(y) = 1/y.

I(y)Ka(y) Ia(y)K'(y) = 1/y.

Step by Step Solution

★★★★★

3.48 Rating (158 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

In cylindrical coordinates the general solution for ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Modern Electrodynamics Questions!

May have unique solutions, an infinite number of solutions, or no solution. Use matrices to find the general solution of each system, if a solution exists. 1. 2. 3. 4. + + z-0 2 2%3D0 (-x+ 2y + 2z...

A relativistic particle with charge q and rest mass mo moves along a circle of radius r in a uniform magnetic field of induction B. Find: (a) The modulus of the particle's momentum vector; (b) The...

Consider a parallel-plate capacitor with charge Q and area A, filled with dielectric material having dielectric constant . It can be shown that the magnitude of the attractive force exerted on each...

python project help appreciated Monte-Carlo transport project Simulate electron transport in a cylindrical Geiger counter filled with Helium gas. This project attempts to simulate the microscopic...

Lecture - Electric Field Lines We have been finding the electric field vector of source charges at a single point in space There are electric field vectors at all points in space surrounding source...

https://phet.colorado.edu/sims/html/charges-and-fields/latest/charges-and-fields_en.html Lecture - Electric Field Lines We have been finding the electric field vector of source charges at a single...

Please help with parts h-j ONLY show all steps to get a good rating. (b) (C) (d) (f) (g) (h) Eumh\" point at. some location P on the zaxis at. height. a > f]? (ii) What must. the value of Emmwtz = 0)...

(b) (C) (d) (f) (g) (h) Eumh\" point at. some location P on the zaxis at. height. a > f]? (ii) What must. the value of Emmwtz = 0) be at the center of the washer? Explain your reasoning. What is the...

Calculus 3 Sections 12.1 and 12.2 Reading Assignment: 3D Coordinates and Vectors Answer Only Exercise 1 by using a screenshot provided Calculus Pearson textbook. Make sure you read these three...

806 Chapter Fifteen OPTIMIZATION: LOCAL AND GLOBAL EXTREMA If f is not continuous or the region R is not closed and bounded, there is no guarantee that f achieves a global maximum or global minimum...

A considerable portion of the tests of controls and substantive tests of transactions are performed simultaneously as a matter of audit convenience. But the substantive tests of transactions...

Sales are normally recorded on the date of the a. Customer purchase order. b. Bill of lading. c. Sales invoice. d. Payment check.

On January 1 2 0 1 6 Knorr Corporation issued 1 0 0 0 0 0 0 of 9 5 year bonds dated January 1 2 0 1 6 The bonds pay interest annually on December 3 1 The bonds were issued to yield 1 0 Bond issue...

Consider the following regression model: where: The following estimated regression equation was obtained from a sample of 30 observations: a. Provide the estimated regression equation for instances...

The three forces (magnitudes 100 lb, 200 lb, and P) combine to produce a resultant R (Figure P4.9). The three forces act in known directions, but the numerical value P is unknown. (a) What should the...

Find a real physical example of a mechanical structure or machine that has a moment acting on it. (a) Make a clear, labeled drawing of the situation. (b) Estimate the dimensions, and the magnitudes...

Resulting from a light wind, the air pressure imbalance of 100 Pa acts across the 1.2-m by 2-m surface of the highway sign (Figure P4.11, see on page 172). (a) Calculate the magnitude of the force...

Problem 11-7 Calculating Annual Shareholder Return and Annual Average Compound Return [LO3] Two years ago, you purchased 100 shares of a cola company. Your purchase price was $52 a share, plus a...

Transaction costsIn late December you decide to sell a losing position that you hold in Twitter so you can capture the loss and use it to offset some capital gains, thus reducing your taxes for the...

7- If the company has a target WACC of 9%, knowing that it can issue bonds at rate of 8% and maintain Beta leverage 1.35, how much approximately it should use equity as portion of its total capital...