A frame tent has a square of side 2 m and two semicircular cross members, FBE and GBD, as shown in Figure 8 88 (a) Show that the cross section ABC has equation 2x 2 z 2 2 (b) Show that the capacity of the tent is 82 3m 3 Figure 8 88 (c) Show that the surface area S m 2 of the tent is given by (d) S...

A frame tent has a square of side 2 m and two semicircular cross members, FBE and

Question:

A frame tent has a square of side 2 m and two semicircular cross members, FBE and GBD, as shown in Figure 8.88.

(a) Show that the cross-section ABC has equation 2x² + z² = 2

(b) Show that the capacity of the tent is 8√2/3m³.

Figure 8.88

F G B D E [T]

5=8 ( * /(1+) dx S X - Use the substitution t = x to show that S=4f" = 1 + t (1-1) -dt and deduce that S = 2

(d) Show that the length s* m of the arclength AB is given by

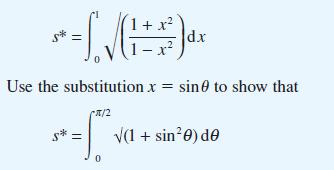
S* * = 1 ( + 1*7) x d.x - Use the substitution x = sine to show that CT/2 "-1","" 0 $* (1 + sin0) de

and evaluate (to 3dp) this integral using the trapezium rule.

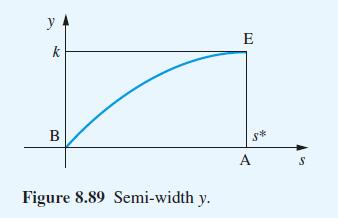
(e) We wish to compute the shape of one of the panels, BDE, of the tent. Show that the semiwidth y, at a distance s from B and illustrated in Figure 8.89, satisfies the differential equation

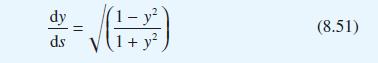
dy ds (1-y 1+y (8.51)

with y = 0 at s = 0.

y k B Figure 8.89 Semi-width y. E $* A S

(f) Show that the slope of the line OR is

1 + y 1- y

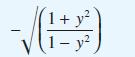
and explain why the construction described in (f) generates an approximate solution to the differential equation.
(g) Use the method to obtain a graphical solution to the differential equation. (Use A4 graph paper with a step size PP´ of 2 cm.)

(h) To use Euler’s method to compute the solution, it is easiest to rescale the independent variable s by setting s = s*t where 0 ≤ t ≤ 1. Show that the initialvalue problem becomes

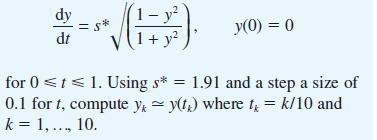
dy dt (1-y 1+ y y(0) = 0 for 0 t 1. Using s* = 1.91 and a step a size of 0.1 fort, compute y y(t) where t =