Use Leibnizs theorem (Question 71) to find the following Data from Question 71 If y u(x)v(x), prove that Hence prove Leibnizs theorem for the nth derivative of a product (a) d dxs (x sin x) (put u sin x, v x) d dx(3x 1) (b) (re ) d4 d x4...

Use Leibnizs theorem (Question 71) to find the following: Data from Question 71 If y = u(x)v(x),

Question:

Use Leibniz’s theorem (Question 71) to find the following:

(a) d dxs (x sin x) (put u = sinx, v = x) d dx(3x + 1)] (b) (re ) d4 d.x4

Data from Question 71

If y = u(x)v(x), prove that

(a) y(x) = u(x)v(x) + 2u(x)v(x) + u(x)v)(x) (b) y(x) = u(x)v(x) + 3u2(x)v(x) + 3u(x)v(x) + u(x)v(x)

Hence prove Leibniz’s theorem for the nth derivative of a product:

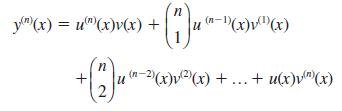
n y")(x) = u"(x)v(x) + (1) (-2)(x) n +(2) -u) (n-1)(x)v()(x) 1-)(x)v()(x) + ... + u(x)v")(x)

Fantastic news! We've Found the answer you've been seeking!

Step by Step Answer:

Answer rating: 100% (QA)

a b c d x sinx sin x3...View the full answer

Answered By

JAPHETH KOGEI

Hi there. I'm here to assist you to score the highest marks on your assignments and homework. My areas of specialisation are: Auditing, Financial Accounting, Macroeconomics, Monetary-economics, Business-administration, Advanced-accounting, Corporate Finance, Professional-accounting-ethics, Corporate governance, Financial-risk-analysis, Financial-budgeting, Corporate-social-responsibility, Statistics, Business management, logic, Critical thinking, So, I look forward to helping you solve your academic problem. I enjoy teaching and tutoring university and high school students. During my free time, I also read books on motivation, leadership, comedy, emotional intelligence, critical thinking, nature, human nature, innovation, persuasion, performance, negotiations, goals, power, time management, wealth, debates, sales, and finance. Additionally, I am a panellist on an FM radio program on Sunday mornings where we discuss current affairs. I travel three times a year either to the USA, Europe and around Africa. As a university student in the USA, I enjoyed interacting with people from different cultures and ethnic groups. Together with friends, we travelled widely in the USA and in Europe (UK, France, Denmark, Germany, Turkey, etc). So, I look forward to tutoring you. I believe that it will be exciting to meet them.

3.00+ 2+ Reviews 10+ Question Solved

Related Book For book-img-for-question

Modern Engineering Mathematics

ISBN: 9781292253497

6th Edition

Authors: Glyn James

See More Books

Question Posted: Jan 13, 2024 09:06 AM

See More Questions

Use Leibnizs theorem (Question 71) to find the following: Data from Question 71 If y = u(x)v(x),

Question:

(a) d dxs (x sin x) (put u = sin .x, v = x) d dx(3x + 1)] (b) (re ) d4 d.x4

Step by Step Answer:

a b c d x sinx sin x3...View the full answer

Modern Engineering Mathematics

Students also viewed these Sciences questions