Show that the group-element commutator \(R_{y}(\delta \theta) R_{x}(\delta \theta) R_{y}^{-1}(\delta \theta) R_{x}^{-1}(\delta \theta)\), is related to the generator commutator \(\left[J_{x}, J_{y}\right]\) by

where the group elements and generators are related by \(R_{x}(\theta)=\exp \left(i J_{x} \theta\right)\) and \(R_{y}(\theta)=\exp \left(i J_{y} \theta\right)\) for a rotation angle \(\theta\). Keep the first three terms of

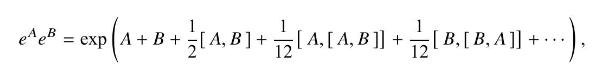
which is called the Baker-Campbell-Hausdorff (BCH) formula.

Transcribed Image Text:

[Jx, Jy] = 80 [1-R, (80) R, (50)R,' (80)R,' (80)],