Question: Consider the 2 x 2 matrix defined by where a 0 is a real number and a is a three dimensional vector with real components.

Consider the 2 x 2 matrix defined by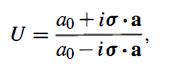 U= = ao + io.a ao-io a

where a₀ is a real number and a is a three dimensional vector with real components.

(a) Prove that U is unitary and unimodular.

(b) In general, a 2 x 2 unitary unimodular matri x represents a rotation in three dimensions. Find the axis and angle of rotation appropriate for U in terms of a₀ , a₁, a₂, and a₃.

U= = ao + io.a ao-io a

Step by Step Solution

★★★★★

3.44 Rating (163 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

a To prove that a 2x2 matrix U is unitary we need to show that its conjugate transpose U is equal to ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Modern Quantum Mechanics Questions!

A borrower obtains a partially amortizing constant payment mortgage loan for $75,000 at 12 percent for 2 years. Payments are monthly. After the last constant payment, he has to pay $15,000 to payback...

For x a real number and n a positive integer, show that (a) (b) (c) 1= (1+x)" - ("*'(1 + x)*-

A family of curves is given by the equations r = 1 + c sin n, where is a real number and is a positive integer. How does the graph change as increases? How does it change as changes? Illustrate by...

Page 6 of 7 4. (12 points) Math 2333: THQ 09, 23-03-17, 18:19 Indicate which of the following collections of objects form a vector space with the given operations. You do not need to give a detailed...

Answer the question shown below. Notes for reference shown below. \fThe function displays the promptstring, waits for keyboard input, and then returns the value from the keyboard. For example, >>...

1. Describe the possible echelon forms of a nonzero 2 x 2 matrix. (3 Select all that apply. (Note that leading entries marked with a I may have any nonzero value and starred entries ( * ) may have...

Follow the steps given in Machine Learning With R , Chapter 5, section "Example Identifying Risky Bank Loans Using C5.0 Decision Trees." download the credit. csv file from Packt Publishing's website...

Problems : 9,11,24,25,26 Direction : in the exercices 9 and 11 find a basis for the eigenspace corresponding to each listed eigenvalueHello can I have some help here please. Can you write on a sheet...

Answer all questions,,,. sun Cabe (x - 2)) sun (abe (y - 2)) Since we are finding the difference between the computed solution and the exact solution, the smaller number is associated with the method...

2 CS229 Problem Set #4 Solutions log m ! p(x(i) |)p() = log p() + m " log p(x(i) |) i=1 i=1 = log p() + m " log " p(x(i) , z (i) |) log " Qi (z (i) ) i=1 = log p() + log p() + m " z (i) i=1 z (i) m...

A soft drink bottling company is interested in controlling its filling operation. Random samples of size 4 are selected and the fill weight is recorded. Table 7-17 shows the data for 24 samples. The...

A detention pond needs to be designed with a total capacity of 30 ac-in. of storage. The inflow hydrograph for the pond is given in Figure P4-10. Assume that that pond is initially 50% full and...

35. Asurvey of 611 office workers investigated telephone answering practices, including how often each office worker was able to answer incoming telephone calls and how often incoming telephone calls...

Is each requirement achievable in the technical environment that will house the system or product?

Write the charge and mass balances for dissolving CaF 2 in water if the reactions are CaF,(8) = Ca2+ + 2F Ca?+ + H,O = CAOH+ + H* Ca2+ + F = CaF+ CaF2(s) = CaF2(aq) F + H* = HF(aq) HF(aq) + F = HF,

Write charge and mass balances for aqueous Ca 3 (PO 4 ) 2 if the species are Ca 2+ , CaOH + , CaPO - 4 , PO 3- 4 , HPO 2 4 - , H 2 PO - 4 , and H 3 PO 4 .

Using activities, find the concentrations of the major species in 0.10 M NaClO 4 saturated with Mn(OH) 2 . Take the ionic strength to be 0.10 M and suppose that the ion size of MnOH + is the same as...

Road Warrior Corporation began operations early in the current year, building luxury motor homes. During the year, the company started and completed 50 motor homes at a cost of $60,000 per unit. Of...

Quiz Determine the gage pressure at point A in Pa. Is it higher or lower than atmospheric? Take y = 9790 N/m for water and y = 133100 N/m for mercury y = 12 N/m for air 45 cm Air Patm A 30 cm Oil,...

Use the data from the trial balance below to prepare an income statement. Please show your work to receive full credit. Some of the items will be needed and some will not. It can be a single step or...