Consider an infinite-horizon representative-agent economy. The representative agent has Epstein-Zin utility. Consumption, expected future consumption, and returns on all assets are jointly lognormally distributed and homoskedastic.

(a) Show that the expected log return on any asset \(i\) can be written as

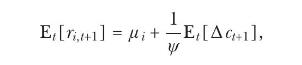
where \(\mu_{i}\) is constant over time and \(c_{t+1}\) denotes log consumption.

(b) We define levered equity as an infinitely-lived asset with dividend equal to \(D_{t}=\) \(C_{t}^{\lambda}\), where \(\lambda\) can be interpreted as a measure of leverage. Use the Campbell-Shiller return decomposition (5.51) to show that the unexpected return to levered equity can be written as

where \(\widetilde{x}_{t+1} \equiv\left(\mathrm{E}_{t+1}-\mathrm{E}_{t}ight) x_{t+1}\) for any variable \(x\) and \(\widetilde{g}_{t+1}\), defined in equation (6.48), captures revisions in expected future consumption growth.

Equation 6.48

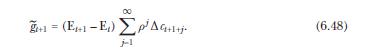
(c) Use the preceding result to derive an expression for the unexpected return on an inflation-indexed perpetuity (real consol bond), an asset with a fixed real dividend every period.
For the remaining parts, assume that aggregate consumption follows an exogenous process given by

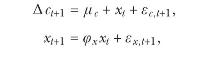
where \(\varepsilon_{c, t+1}, \varepsilon_{x, t+1}\) are iid with zero means with variances \(\sigma_{c}^{2}\) and \(\sigma_{x}^{2}\), and covariance \(\sigma_{c x}\).

(d) Show that the risk premium on levered equity over the riskfree interest rate is given by

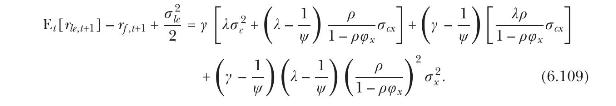
(e) Use the preceding result to obtain expressions for the consol bond risk premium over the riskfree rate and for the risk premium of levered equity over the real consol bond. Interpret each of the terms appearing in the two expressions and give the economic intuition for their sign. What determines the sign of the term premium and the equity premium?

(f) If \(\sigma_{c}^{2}\) and \(\sigma_{c x}\) are small, as the smooth path of observed consumption growth implies, what restrictions on preference parameters \(\gamma\) and \(\psi\) imply both large equity premia and small real term premia (positive or negative)?

Transcribed Image Text:

E[r]=i+E [AC+1], Y