Density of natural boron is \(2.4 \mathrm{~g} / \mathrm{cc}\). Given: \(\sigma_{a}\) of \({ }^{10} \mathrm{~B}=4000 \mathrm{~b}\), and \(\sigma_{a}\) of \({ }^{11} \mathrm{~B}=0 \mathrm{~b}\). If the abundance ratio of \({ }^{10} \mathrm{~B}:{ }^{11} \mathrm{~B}\) is as \(20: 80\), find \(\Sigma_{a}\), and mean free path of neutron in natural boron.

\(\Delta=M-A\) is the "mass excess," where \(M\) is the mass of a nuclide and \(A\) its mass number. These data are given in the Nuclear Wallet cards, and elsewhere. The data given below may be useful in solving some of the problems.

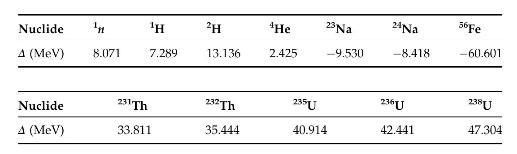
Nuclide n H 2H 4He 23 Na 24Na A (MeV) 8.071 7.289 13.136 2.425 -9.530 -8.418 56Fe -60.601 Nuclide 231 Th 232 Th 235U 236U 238U A (MeV) 33.811 35.444 40.914 42.441 47.304