For X S n , and i {1, . . . , n}, we denote by i(X) the i-th largest eigenvalue of X.

For X ∈ Sⁿ, and i ∈ {1, . . . , n}, we denote by λi(X) the i-th largest eigenvalue of X. For k ∈ {1, . . . , n}, we define the function f_k : Sⁿ → R with values

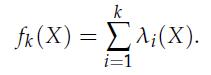
This function is an intermediate between the largest eigenvalue (obtained with k = 1) and the trace (obtained with k = n).

1. Show that for every t ∈ R, we have f_k(X) ≤ t if and only if there exist Z ∈ Sⁿ and s ∈ R such that

2. Show that fk is convex. Is it a norm?
3. How would you generalize these results to the function that assigns the sum of top k singular values to a general rectangular m x n matrix, with k ≤ min(m, n)?

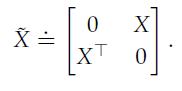
k fk(X) = ;(x). = i=1