In this problem, we consider the calculations for Ï p and Ï x for the particle in the box shown in Figure 17.5 in more

In this problem, we consider the calculations for σ_pand σ_xfor the particle in the box shown in Figure 17.5 in more detail. In particular, we want to determine how the absolute uncertainty Δp_xand the relative uncertainty Δp_x/p_xof a single peak corresponding to either the most probable positive or negative momentum depends on the quantum number n.

a. First we must relate k and p_x. From E = p²_x/2m and E = n²h²/8ma², show that p_x = nh/2a.

b. Use the result from part (a) together with the relation linking the length of the box and the allowed wavelengths to obtain p_x = hk.

c. Relate Δ p_x and Δp_x /p_x with k and Δk.

d. The following graph shows ˆ£A_kˆ£² versus k €“ k _peak . By plotting the results of Figure 17.5 in this way, all peaks appear at the same value of the abscissa. Successive curves have been shifted upward to avoid overlap. Use the width of the ˆ£A_kˆ£² peak at half height as a measure of Δk. What can you conclude from this graph about the dependence of Δp_x on n?

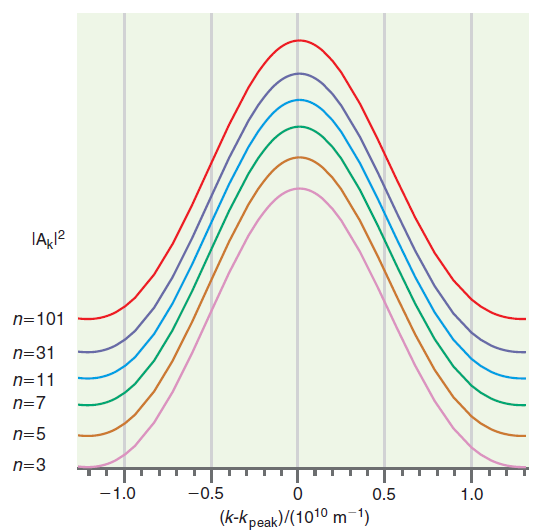
e. The following graph shows ˆ£A_kˆ£² versus k /n for n = 3, n = 5, n = 7, n = 11, n = 31, and n = 101. Use the width of the ˆ£A_kˆ£² peak at half height as a measure of Δk /n. Using the graphs, determine the dependence of Δp_x /p_x on n. One way to do this is to assume that the width depends on n like (Δp_x /p_x) = n^α, where α is a constant to be determined. If this relationship holds, a plot of ln (Δp_x /p_x) versus ln n will be linear and the slope will give the constant α. 

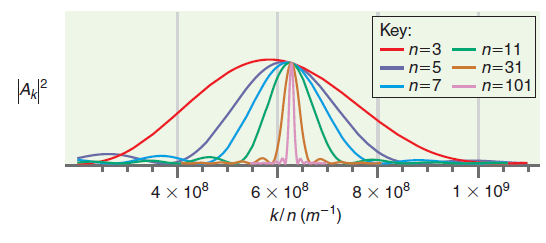
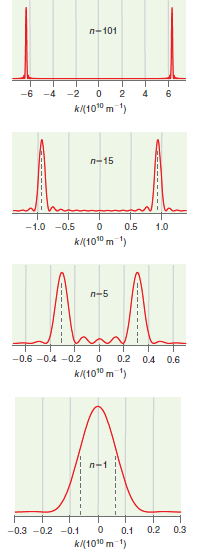
Figure 17.5

n=101 n=31 n=11 n=7 n=5 n=3 0.5 -1.0 -0.5 1.0 (k-kpeak)/(1010 m-1) Key: n=3 n=5 n=7 n=11 n=31 n=101 6 x 108 kln (m-') 4 x 108 8 x 108 1 x 109 2.