Suppose that X1 and X2 are independent random variables having the uniform distribution on (0, 1, 2, 3, 4, 5). That is, f( j) PXi j for i 1, 2 and 0 j 5.

a. Compute E(X1) and Var(X1). [Hint: Use the formulas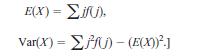

b. Determine the probability distribution for Y X1 X2. [Hint: For each possible value of Y, determine all combinations of X1 and X2 that result in that value. For example, Y 3 can be obtained by (X1, X2) (0, 3), (1, 2), (2, 1), and (3, 0).
Since each pair has probability we obtain PY 3
Repeat this process for all values of Y. As a check be sure that

c. Using the results of part (b), find P1.5 Y 6.5.

d. Using the results E(Y) 2E(X1) and Var(Y) 2Var(X1), approximate the answer to part

(c) using a normal distribution.

e. Suppose that X1, X2, . . . , X20 are independent identically distributed random variables having the uniform distribution on (0, 1, 2, 3, 4, 5). Using a normal approximation, estimate

f. Do you think that the approximation computed in part (d ) or part

(e) is more accurate?
Why?

Transcribed Image Text:

E(X) = i). Var(X) - (E(X))]