5.7. Consider a collection of circles in the plane whose centers are distributed according to a spatial Poisson process with parameter AJAI, where J denotes the area of the set A. (In particular, the number of centers (A)

in the set A follows the distribution law Pr(e(A) = k} = e AA[(A[AJ)'1k!].)

The radius of each circle is assumed to be a random variable independent of the location of the center of the circle, with density functionf(r) and finite second moment.

(a) Show that C(r), defined to be the number of circles that cover the origin and have centers at a distance less than r from the origin, determines a variable-time Poisson process, where the time variable is now taken to be the distance r.

Hint: Prove that an event occurring between r and r + dr (i.e., there is a circle that covers the origin and whose center is in the ring of radius r to r + dr) has probability A27rr dr f ;f(p) dp + o(dr), and events occurring over disjoint intervals constitute independent r.v.'s. Show that C(r)

is a variable-time (nonhomogeneous) Poisson process with parameter

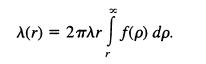
(b) Show that the number of circles that cover the origin is a Poisson random variable with parameter A f o 7rr2f(r) dr.

Transcribed Image Text:

A(r) 2r f(p) dp. =